Uma partícula de massa m executa um Movimento Harmônico Simples (MHS) de amplitude L, ao longo do eixo das abscissas Ox, com centro das oscilações em P não coincidente com O, origem de Ox. O quadrado da velocidade V da partícula guarda, com sua posição x, uma relação funcional curiosa expressa por com A, B e C constantes dadas em unidades do Sistema Internacional (SI).

Sabendo que e que quaisquer efeitos resistivos são negligenciáveis, a amplitude L desse MHS é dada por

Um pêndulo simples é abandonado da posição B e seu movimento é observado até a posição C. O movimento da projeção da sombra da esfera do pêndulo sobre um eixo horizontal, onde são marcadas as posições (x), descreve um movimento harmônico simples, conforme a figura.

Considerando o movimento do pêndulo conservativo, assinale a alternativa que representa corretamente a energia cinética (Ec) referente ao componente horizontal da velocidade do pêndulo em função da posição x.

Considere que

I – a esfera possui massa igual a “m”;
II – o cabo tem massa desprezível;
III – a pulsação do movimento é representado por “ω” e
IV – as projeções dos pontos B e C no eixo “x” são, respectivamente, as posições -A e A. 

Sobre uma superfície horizontal, que não oferece atrito, repousa um bloco de dimensões desprezíveis e de 4,0kg de massa. Uma mola de constante 400N/m, disposta horizontalmente, tem uma extremidade presa a uma parede e outra extremidade presa ao bloco. O sistema bloco + mola é posto a oscilar e seu movimento é descrito pela equação horária

  x(t) = (0,04m) cos(10t – π), com t, em segundos.

De acordo com os conhecimentos de movimento harmônico simples, é correto afirmar que a máxima energia cinética desse oscilador vale:

Um professor faz um experimento para demonstrar a relação entre a frequência de oscilação de um pêndulo simples e o comprimento desse pêndulo. Para isso, segura uma extremidade de um fio de massa desprezível que está apoiado em um pino horizontal fixo em uma parede, de modo que o comprimento suspenso desse fio meça 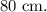Nessa situação, uma pequena esfera, presa a outra extremidade desse fio, oscila em um plano vertical, entre os pontos P e Q, com uma frequência de oscilação f₀.

Em determinado Instante do movimento oscilatório, O professor puxa o fio movimentando sua mão horizontalmente para a direita com velocidade constante de 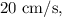durante 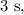e o fio desliza sobre o pino.

Considerando que o período de oscilação desse pêndulo possa ser calculado com a expressão 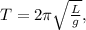 em que L é o comprimento do pêndulo e g é a aceleração da gravidade local, ao final do intervalo de 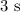a nova frequência de oscilação desse pêndulo será:

Um sensor detecta oscilações na superfície da Terra e as transmite a um sismógrafo. Ao registrar a amplitude das ondas em função do tempo t, este equipamento gera um sismograma.

O traçado de um sismograma hipotético é fornecido pelo gráfico da função y(t) = A + B sen(𝜔𝑡), onde 𝜔 é a frequência angular da perturbação, e cuja amplitude é dada por

Uma mola ideal tem uma de suas extremidades presa em uma parede e a outra conectada a um bloco, ambos colocados sobre uma superfície horizontal, com a mola em seu comprimento natural, como mostra a figura 1. Em seguida, o bloco é deslocado até a posição mostrada na figura 2.

Figura 1

Figura 2

No instante t = 0, o bloco, ainda na posição mostrada na figura 2, é abandonado, a partir do repouso, e passa a se deslocar em movimento harmônico simples com frequência igual a 20 Hz.

A equação que descreve esse movimento no referencial do eixo x, em função do tempo e em unidades do Sistema Internacional de Unidades, é: