Questões de Matemática - Álgebra - Equações polinomiais - Relações de Girard
280 Questões
Se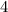 
é uma das raízes do polinômio %20%3D%20x%5E3%20-%208x%5E2%20%2B%2019x%20-%2012)
, então as outras raízes são números
Considerando que, na unidade de pronto-socorro de um hospital, quatro médicos façam atendimento aos pacientes e que haja a mesma probabilidade de esses pacientes serem atendidos por qualquer um desses médicos.
Considere que a quantidade de dias semanais em que cada um dos médicos atende no pronto socorro corresponda, respectivamente, a cada uma das raízes reais do polinômio p(x) = (x-2).(x3 - 6x2 + 11x - 6)
Nesse caso, se, nos dias de atendimento, cada um dos médicos atender durante 6 horas, então a quantidade total de horas semanais disponibilizadas pelos quatro médicos será superior a 40 horas.
Considere o polinômio P(x) x4 - 3x3 - 3x2 + 7x + 6.
Sabendo-se que -1 é raiz dupla da equação P(x) = 0, as outras raízes dessa equação são
A grande pirâmide de Giza, construída para o faraó Khufu, em 2694 a.C., é uma façanha da arquitetura e engenharia que atrai, há séculos, a imaginação e curiosidade dos mais diversos povos. Ela possui 2.300.000 blocos, cujos pesos variam entre 2,5 e 80 toneladas, e levou 20 anos para ser construída. Do ponto de vista da matemática, a pirâmide de Khufu é uma obra fascinante, pelo fato de se aproximar de uma pirâmide áurea. A razão áurea desperta bastante curiosidade por ter sido associada a uma estética agradável e por ter relações com outros objetos matemáticos como a sequência de Fibonacci, definida por fn+2 = fn + fn+1, para todo n ≥ 1, com f1 = f2 = 1. Uma pirâmide reta de base quadrada será áurea se a razão entre apótema de uma face lateral e a metade da aresta da base for a razão áurea , que corresponde à raiz positiva da equação r2 - r - 1 = 0. A figura seguinte ilustra uma pirâmide reta de base quadrada que possui as mesmas proporções da grande pirâmide de Giza.
Considerando o texto e a imagem precedentes, julgue o item a seguir.
Se ψ é a raiz negativa da equaç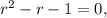ão 
então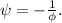 
A soma e o produto dos valores de 𝑥, que tornam a equação 4𝑥3 − 36𝑥2 + 5𝑥 + 2 = 0 verdadeira, são, respectivamente:
Sendo x1 e x2 as raízes da equação x2 – 5x + 6 = 0, o resultado do produto x1 x2 é:
Adicionar à pastas
06
