Questões de Matemática - Números - Conjuntos - Conjunto dos números complexos
Seja o número complexo:
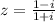
Então, 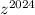 é igual a:
é igual a:
Considere os afixos dos sete números complexos indicados no plano de Argand-Gauss.

Dado %2C) o afixo do número complexo W Y + Z é
o afixo do número complexo W Y + Z é

Na área da reserva ambiental representada na figura anterior, foi inserido um sistema de coordenadas cartesianas ortogonais xOy, no qual são definidos os pontos A = (-2, 0), B = (–1, 4), C = (2, 3), D = (2, -2) e E = (-2, -2).
Cada ponto (a, b) desse plano cartesiano é identificado com o número complexo z = a + bi, em que a unidade imaginária i é tal que i2 = -1.
Se ZC é o número complexo que representa o ponto C, então (ZC)2 = 5 + 12i.
Se m é o número que torna o complexo 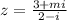 um imaginário puro, então o valor de
um imaginário puro, então o valor de 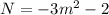 é:
é:
As raízes complexas de polinômios estão relacionadas com os vértices de polígonos. A figura a seguir ilustra o plano de Argand-Gauss e duas circunferências, de raios 1 e 3, respectivamente, centradas na origem. Na figura, os pontos z1, ..., z12 são as raízes complexas da equação z12 − 312 = 0 e são os vértices do polígono estrelado.

Considerando essas informações, julgue o item.
Os pontos 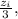 para
para 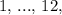 são as raízes complexas da equação
são as raízes complexas da equação 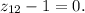
Considere k um número real negativo e 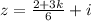 um número complexo, em que i é a unidade imaginária.
um número complexo, em que i é a unidade imaginária.
Nessas condições, o valor de k, de modo que 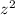 seja imaginário puro, é
seja imaginário puro, é





