Questões de Matemática - Geometria - Trigonometria
A figura a seguir ilustra, no sistema de coordenadas ortogonais xOy, a situação em que uma partícula é lançada com uma velocidade inicial v0 =10 m/s no sentido positivo do eixo-+, em direção ao arco de circunferência localizado no segundo quadrante do sistema de coordenadas e cujo centro é o ponto C. A partícula passa dessa trajetória para o arco de curva no primeiro quadrante do sistema, de maneira exata na figura, α = π/3, r = 2 m e d = 4 m.

A partir dessas informações e considerando que não há atrito em toda a trajetória da partícula e que %3D%5Cfrac%7B%5Csqrt%7B3%7D%7D%7B2%7D) e
e %3D%5Cfrac%7B1%7D%7B2%7D%2C) julgue o item.
julgue o item.
No que se refere à figura, comparando-se a parábola que a partícula irá traçar em sua trajetória no segundo quadrante do sistema de coordenadas com o ponto em que a reta pontilhada cruza o eixo-y, verifica-se que a altura máxima atingida pela partícula será inferior a 1 + 2 tg (β).
Uma matriz em duas dimensõesA2 ×2 é uma matriz de rotação quando a multiplicação de um par ordenado V(x, y) na forma de matriz coluna 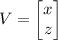 por A produz como resultado um vetor
por A produz como resultado um vetor 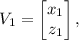 que pode ser identificado com o par ordenado
que pode ser identificado com o par ordenado ) cuja distância à origem é a mesma que V. Nesse contexto, seja a matriz A abaixo, em que a ∈ℝ.
cuja distância à origem é a mesma que V. Nesse contexto, seja a matriz A abaixo, em que a ∈ℝ.
![]()
Considere que a matriz A faça uma rotação por um ângulo α em um ponto P(x, y) do plano, na seguinte forma.
![]()
Então 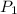 (xcos (α) + ysen(α), - xsen (α) + ycos (α)) é o ponto obtido de pela rotação de P, em torno da origem, por um ângulo α
(xcos (α) + ysen(α), - xsen (α) + ycos (α)) é o ponto obtido de pela rotação de P, em torno da origem, por um ângulo α
Tendo como referência essas informações, julgue o item.
A2 = A.A é a matriz obtida quando se efetua uma rotação por um ângulo 2.α.
Uma matriz em duas dimensõesA2 ×2 é uma matriz de rotação quando a multiplicação de um par ordenado V(x, y) na forma de matriz coluna 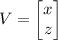 por A produz como resultado um vetor
por A produz como resultado um vetor 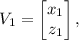 que pode ser identificado com o par ordenado
que pode ser identificado com o par ordenado ) cuja distância à origem é a mesma que V. Nesse contexto, seja a matriz A abaixo, em que a ∈ℝ.
cuja distância à origem é a mesma que V. Nesse contexto, seja a matriz A abaixo, em que a ∈ℝ.
![]()
Considere que a matriz A faça uma rotação por um ângulo α em um ponto P(x, y) do plano, na seguinte forma.
![]()
Então 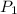 (xcos (α) + ysen(α), - xsen (α) + ycos (α)) é o ponto obtido de pela rotação de P, em torno da origem, por um ângulo α
(xcos (α) + ysen(α), - xsen (α) + ycos (α)) é o ponto obtido de pela rotação de P, em torno da origem, por um ângulo α
Tendo como referência essas informações, julgue o item.
Se α = –π/2, então o ponto ) é rotacionado no sentido anti-horário para o segundo quadrante.
é rotacionado no sentido anti-horário para o segundo quadrante.
As medidas, expressas em graus, dos ângulos internos de um triângulo retângulo constituem uma progressão aritmética.
Se x é a medida de um dos ângulos agudos deste triângulo, então, tg(x) pode ser igual a
Palmas tem várias opções de praias de água doce e uma das mais conhecidas é a Praia da Graciosa. A mesma está localizada próxima ao centro da cidade com uma extensa orla, banhada pelo Lago de Palmas e ao lado da Ponte Fernando Henrique Cardoso, também conhecida como Ponte da Amizade e da Integração. A Ilha Canela fica localizada no Lago de Palmas e próxima à Praia da Graciosa.
Um turista no ponto C da Praia da Graciosa, conforme figura a seguir, observa dois extremos A e B sob um ângulo de 60º, onde o ponto A é a Ilha Canela e o ponto B é o centro da ponte da Amizade e da Integração. Sabe-se que as distâncias de A e B até C são, respectivamente, 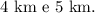

Com base nessas informações, é CORRETO afirmar que a distância entre a Ilha Canela e o centro da Ponte da Amizade e da Integração é:
O pai de Pedro está posicionado na praia num ponto C e observa seu filho no mar, em um ponto A, distante 10m de onde o pai está. No mesmo instante, um salva vidas se encontra em um ponto B, distante 15m desse pai, de tal modo que o ângulo ACB=60°.
Dado: Lei dos cossenos a2 = b2 + c2 - 2bc.cosÂ
A distância entre o salva vidas e o garoto nesse instante é de aproximadamente

Faça seu login GRÁTIS
Minhas Estatísticas Completas
Estude o conteúdo com a Duda
Estude com a Duda
Selecione um conteúdo para aprender mais:





