Questões de Matemática - Geometria - Trigonometria - Função Seno
A figura a seguir ilustra, no sistema de coordenadas ortogonais xOy, a situação em que uma partícula é lançada com uma velocidade inicial v0 =10 m/s no sentido positivo do eixo-+, em direção ao arco de circunferência localizado no segundo quadrante do sistema de coordenadas e cujo centro é o ponto C. A partícula passa dessa trajetória para o arco de curva no primeiro quadrante do sistema, de maneira exata na figura, α = π/3, r = 2 m e d = 4 m.

A partir dessas informações e considerando que não há atrito em toda a trajetória da partícula e que %3D%5Cfrac%7B%5Csqrt%7B3%7D%7D%7B2%7D) e
e %3D%5Cfrac%7B1%7D%7B2%7D%2C) julgue o item.
julgue o item.
No que se refere à figura, comparando-se a parábola que a partícula irá traçar em sua trajetória no segundo quadrante do sistema de coordenadas com o ponto em que a reta pontilhada cruza o eixo-y, verifica-se que a altura máxima atingida pela partícula será inferior a 1 + 2 tg (β).
A figura seguinte mostra a tela, em determinado instante, de um antigo video game: os foguetes, representados pelas letras de A a G, deveriam ser destruídos por tiros disparados a partir do controle remoto.

Na tela, foi inserido um sistema de coordenadas cartesianas ortogonais xOy. Para cada foguete, foi estabelecida a sua posição no sistema, conforme as coordenadas mostradas na tabela seguinte.

Cada ponto (x, y) desse sistema de coordenadas é identificado com o número complexo x + iy, em que a unidade imaginária i é tal que i2 = -1.
Tendo como referência a situação precedente, julgue o item.
O número complexo %2Bi%5Ccdot%20sen%5C(%20%5Cfrac%20%7B%5Cpi%7D%7B4%7D%5C)%20%5Cright%5D) está associado à posição do foguete B.
está associado à posição do foguete B.
Raios de luz solar estão atingindo a superfície de um lago formando um ângulo x com a sua superfície, conforme indica a figura.
Em determinadas condições, pode-se supor que a intensidade luminosa desses raios, na superfície do lago, seja dada aproximadamente por l(x) = k • sen(x)
sendo k uma constante, e supondo-se que x está entre 0o e 90°.

Quando x = 30°, a intensidade luminosa se reduz a qual percentual de seu valor máximo?

A figura representa o traçado de uma pista, planejada por um engenheiro urbanista, a qual ligará o ponto M ao ponto N, da mesma cidade.
Para tal, o engenheiro inspirou-se no gráfico da função trigonométrica, com arco variando no intervalo [0, 2
π],
Por meio de um estudo, verificou-se que a temperatura média mensal em Boa Vista no período de 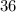 meses, de
meses, de 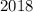 a
a 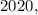 pode ser modelada pela função F(t) a seguir, com valor em graus Celsius.
pode ser modelada pela função F(t) a seguir, com valor em graus Celsius.
%3D3%5C%20sen%5Cleft%5B%5Cfrac%7B%5Cpi%7D%7B3%7D%5Cleft(t-1%5Cright)%5Cright%5D%2B30)
Nessa função, t pertence ao intervalo 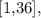
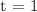 corresponde ao mês de janeiro de
corresponde ao mês de janeiro de 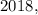
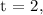 ao mês de fevereiro de
ao mês de fevereiro de 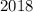 e assim sucessivamente.
e assim sucessivamente.
De acordo com esse estudo, a temperatura média mensal em Boa Vista durante o período observado foi
Na Figura estão representados os gráficos das funções cosseno e seno definidas no intervalo 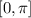 .
.

Considerando os pontos A, B e C mostrados na Figura, o triângulo com vértices A, B e C tem área igual a:
Faça seu login GRÁTIS
Minhas Estatísticas Completas
Estude o conteúdo com a Duda
Estude com a Duda
Selecione um conteúdo para aprender mais:





