Questões de Matemática - Geometria - Trigonometria - Função Coseno
A figura seguinte mostra a tela, em determinado instante, de um antigo video game: os foguetes, representados pelas letras de A a G, deveriam ser destruídos por tiros disparados a partir do controle remoto.

Na tela, foi inserido um sistema de coordenadas cartesianas ortogonais xOy. Para cada foguete, foi estabelecida a sua posição no sistema, conforme as coordenadas mostradas na tabela seguinte.

Cada ponto (x, y) desse sistema de coordenadas é identificado com o número complexo x + iy, em que a unidade imaginária i é tal que i2 = -1.
Tendo como referência a situação precedente, julgue o item.
O número complexo %2Bi%5Ccdot%20sen%5C(%20%5Cfrac%20%7B%5Cpi%7D%7B4%7D%5C)%20%5Cright%5D) está associado à posição do foguete B.
está associado à posição do foguete B.
É comum que os índios realizem o tempo de plantio de acordo com as fases da lua. Supondo-se que as fases da lua podem ser modeladas, aproximadamente, pela função %3D0%2C5%2B0%2C5sen%5Cleft(%5Cfrac%7B%5Cpi%20d%7D%7B14%7D%5Cright)) , onde 𝒇(𝒅) corresponde à fração da superfície da lua, visível e iluminada no 𝒅-ésimo dia de uma observação. Nessas condições, o período da função 𝒇 é dado por
, onde 𝒇(𝒅) corresponde à fração da superfície da lua, visível e iluminada no 𝒅-ésimo dia de uma observação. Nessas condições, o período da função 𝒇 é dado por
A variação da pressão sanguínea (em mmHG) de uma pessoa em função do tempo (em segundos) é uma função trigonométrica cuja lei é dada por :
%3D100-20.cos%5Cleft(%5Cfrac%7B8%5Cpi%7D%7B3%7Dt%5Cright))
De acordo com os dados acima, assinale a alternativa que corresponde à CORRETA variação da pressão
A razão entre o maior e o menor número inteiro que pertencem ao conjunto imagem da função trigonométrica 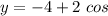
) é
é

A figura acima ilustra um brinquedo de base arredondada denominado joão-bobo. Por mais que o inclinem, ele tende a retornar à sua posição de equilíbrio, permanecendo de pé. Considere que um joão-bobo, ao ser inclinado, execute movimentos oscilatórios de pequenas amplitudes. Considere, ainda, que, para descrever o deslocamento horizontal, em centímetros, da cabeça do joão-bobo durante os movimentos oscilatórios, foram propostos dois modelos distintos, conforme expressões a seguir, em que f e g expressam o deslocamento horizontal do ponto A posicionado no topo da cabeça do brinquedo e o tempo 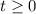 é medido em segundos. Considere, por fim, que, no que se refere a esses modelos, o ponto A realize movimento apenas no plano e que o brinquedo está na posição de equilíbrio quando a posição escalar horizontal do ponto A é nula.
é medido em segundos. Considere, por fim, que, no que se refere a esses modelos, o ponto A realize movimento apenas no plano e que o brinquedo está na posição de equilíbrio quando a posição escalar horizontal do ponto A é nula.
Primeiro modelo: f(t) = 20cos[π(t + 1)] cm
Segundo modelo: g(t) = 202-t cos[π(t + 1)] cm
Tendo como referência essas informações, julgue o item.
De acordo com o primeiro modelo, um movimento completo de ida e volta do joão-bobo ocorre em 2 s.

A figura representa o traçado de uma pista, planejada por um engenheiro urbanista, a qual ligará o ponto M ao ponto N, da mesma cidade.
Para tal, o engenheiro inspirou-se no gráfico da função trigonométrica, com arco variando no intervalo [0, 2
π],
Faça seu login GRÁTIS
Minhas Estatísticas Completas
Estude o conteúdo com a Duda
Estude com a Duda
Selecione um conteúdo para aprender mais:





