Questões de Matemática - Geometria - Trigonometria - Equações trigonométricas
Uma matriz em duas dimensõesA2 ×2 é uma matriz de rotação quando a multiplicação de um par ordenado V(x, y) na forma de matriz coluna 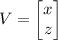 por A produz como resultado um vetor
por A produz como resultado um vetor 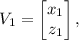 que pode ser identificado com o par ordenado
que pode ser identificado com o par ordenado ) cuja distância à origem é a mesma que V. Nesse contexto, seja a matriz A abaixo, em que a ∈ℝ.
cuja distância à origem é a mesma que V. Nesse contexto, seja a matriz A abaixo, em que a ∈ℝ.
![]()
Considere que a matriz A faça uma rotação por um ângulo α em um ponto P(x, y) do plano, na seguinte forma.
![]()
Então 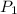 (xcos (α) + ysen(α), - xsen (α) + ycos (α)) é o ponto obtido de pela rotação de P, em torno da origem, por um ângulo α
(xcos (α) + ysen(α), - xsen (α) + ycos (α)) é o ponto obtido de pela rotação de P, em torno da origem, por um ângulo α
Tendo como referência essas informações, julgue o item.
A2 = A.A é a matriz obtida quando se efetua uma rotação por um ângulo 2.α.
O gráfico a seguir representa a função periódica definida por f(x) = 2sen(x), x ∈ R. No intervalo 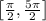 , A e B são pontos do gráfico nos quais
, A e B são pontos do gráfico nos quais %3Df%5Cleft(%5Cfrac%7B5%5Cpi%7D%7B2%7D%5Cright)) são valores máximos dessa função.
são valores máximos dessa função.

A área do retângulo ABCD é:
Parte do gráfico da função f(x) = 1 + 2. sen(2x) está representado na Figura abaixo.

O conjunto imagem Im(f) e o período p dessa função são:
É comum que os índios realizem o tempo de plantio de acordo com as fases da lua. Supondo-se que as fases da lua podem ser modeladas, aproximadamente, pela função %3D0%2C5%2B0%2C5sen%5Cleft(%5Cfrac%7B%5Cpi%20d%7D%7B14%7D%5Cright)) , onde 𝒇(𝒅) corresponde à fração da superfície da lua, visível e iluminada no 𝒅-ésimo dia de uma observação. Nessas condições, o período da função 𝒇 é dado por
, onde 𝒇(𝒅) corresponde à fração da superfície da lua, visível e iluminada no 𝒅-ésimo dia de uma observação. Nessas condições, o período da função 𝒇 é dado por
Sendo A= 12 + sen2x + cos2x , 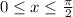 , é CORRETO afirmar que:
, é CORRETO afirmar que:
Raios de luz solar estão atingindo a superfície de um lago formando um ângulo x com a sua superfície, conforme indica a figura.
Em determinadas condições, pode-se supor que a intensidade luminosa desses raios, na superfície do lago, seja dada aproximadamente por l(x) = k • sen(x)
sendo k uma constante, e supondo-se que x está entre 0o e 90°.

Quando x = 30°, a intensidade luminosa se reduz a qual percentual de seu valor máximo?
Faça seu login GRÁTIS
Minhas Estatísticas Completas
Estude o conteúdo com a Duda
Estude com a Duda
Selecione um conteúdo para aprender mais:





